As discussed previously, prediction is essential to survival. No living creature could cope with pure randomness. We depend on the sun rising tomorrow. We depend on the seasons of the year to grow food. We need to be able to predict where to find water. Imagine what life would be like if the temperature fluctuated randomly, perhaps minute by minute, over a range of hundreds of degrees. Life couldn't survive -- at least not life as we know it. So there is some order to our world. Order means stability and continuity, which allows prediction. Prediction allows decisions. And good decisions are at the heart of survival and quality of life. It is logical to suppose that there are some universal laws that govern our environment. To the extent that we can discover those laws and understand them, we have the potential of improving the success of our lives, no matter how you want to measure success.
In order to address the question of stability, it is necessary to consider some basic attributes of a system. A system is made up of individual parts that interact. How they interact is the difference between random chaos and some level of stability or a high level of order. By way of example, let us consider a simple system. Picture in your mind a man standing in an empty field. Suppose the man has a totally free will and can move about as he pleases. To simplify the situation we shall limit the movement to a single dimension and say the man always has three choices: each time he picks up his foot he can 1) place it forward in front of his other foot [advance], 2) place it next to his other foot [stand still], or 3) he can reverse direction and effectively step backward [retreat]. Expressed mathematically, we have three rules: on each step the man can go forward one (1), stay at zero (0), or go back one (-1). If he takes one hundred steps, he could be forward one hundred paces, back one hundred paces, or anywhere in between (because he can change his mind about his intention on any step). The task is to predict where he will be in one hundred steps. The fact is that since he could be anywhere within a two hundred pace range there is no way of knowing where he will be. But wait. Probability theory should help predict where he might be.
What do we know about probability theory? There is only one way the man could get one hundred paces ahead and only one way he could get one hundred paces back. In either case, the man would have to consistently move in the same direction on every step. So out of all the possibilities, it is unlikely that he would be at either extreme end of the range. It is more likely that he would be somewhere between the extremes. In fact, it is possible to diagram out each step.
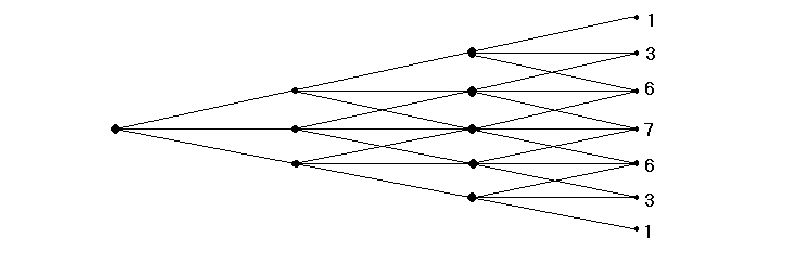 |
On the first step the chances are 1/3 that he could be in any one of three positions. By the second step the chances are still 1/3 that he could be in the middle because there are three out of nine ways to get there, but only one out of nine that he will be at either extreme. The pattern should be obvious. By the third step it is less likely that he is still exactly where he started, but the probabilities are better than 70% that he has moved one step or less in either direction. No matter how many steps he is allowed, the greatest probability is that he will be at or close to where he started. Of course this assumes that his choice of steps is random each time. We could plot all the probabilities and come up with a typical bell curve. We could compute standard deviations and make some general statements about the man's likely position after 100 steps.
 |
Probability theory is useful when you are dealing with a group of men, or one man repeating an event multiple times. But if you only have one chance at finding the man in the field, probability won't help you much. You can improve your odds of guessing where he might be, but it is unlikely that you can pick the exact spot. Picture a man standing in front of Saint Peter at the pearly gates of heaven. Saint Peter is explaining to him, "I know they told you back on earth the odds of dying that way were only one in ten million -- and they were right -- but you are that one in ten million'."
Let's change the example to a shape located in space. I am going to use a circle, and we will assume that the circle is defined by a perimeter of discreet dots or objects. We will call these things molecules. Using a computer is it easy to create a graphical representation of a perfect circle with a radius of 100 units.
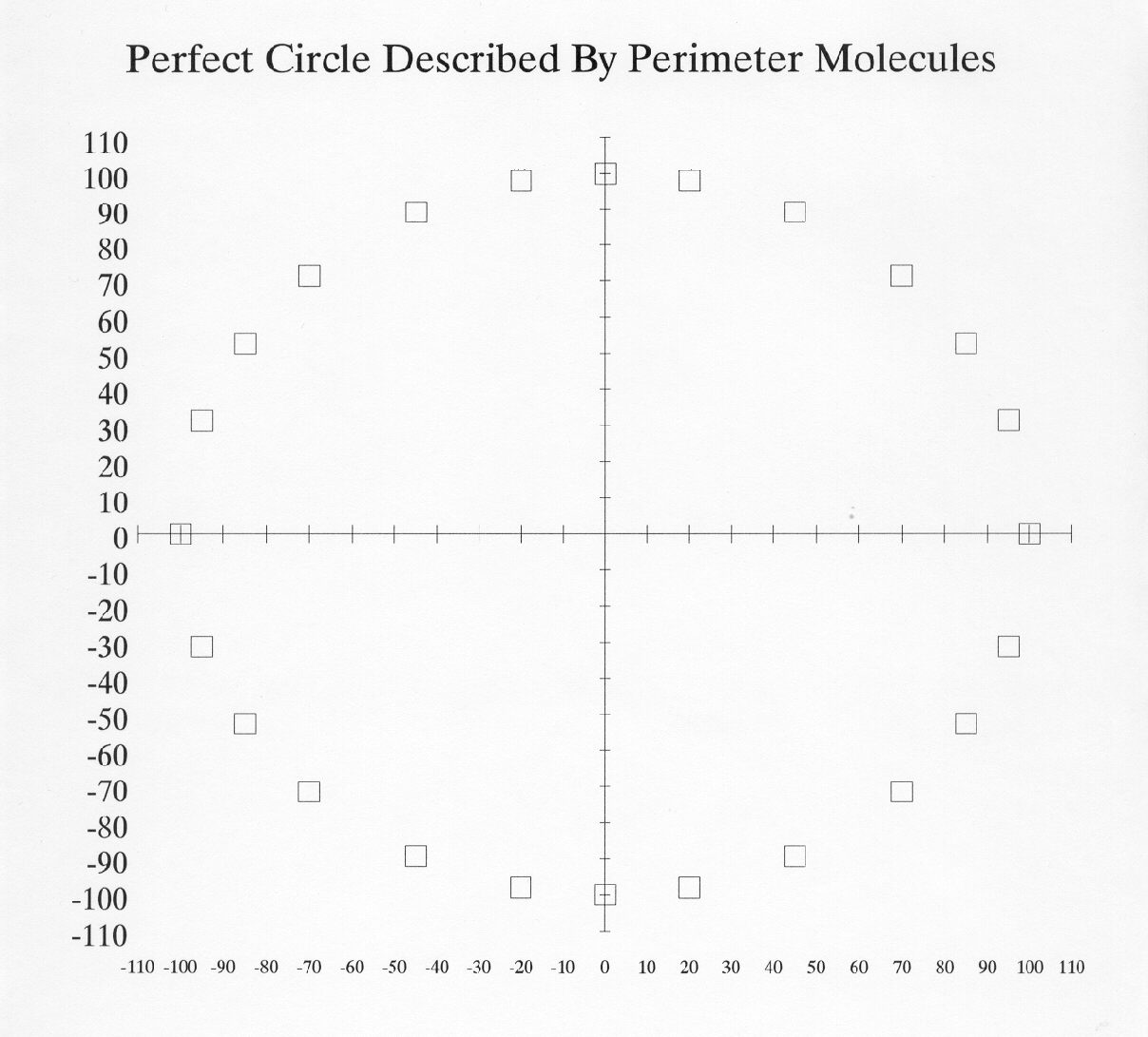 |
Let us suppose that each molecule can act entirely independently, just like the man in the field. It is very simple to program the computer with a random number generator to mimic what might happen to each molecule on each move. Some molecules will move in toward the center of the circle, some stay in place, and some may move outward. Common sense would lead us to believe that if there is nothing holding the molecules in place, the shape of the circle will break down fairly quickly.
Now recall what probability predicts. In is unlikely that any molecule will move to an extreme. The odds favor the majority of the points clustering near their original position. So after one hundred random moves we still have a recognizable circle. The intuitive belief that the shape of the circle should break down rapidly is incorrect!
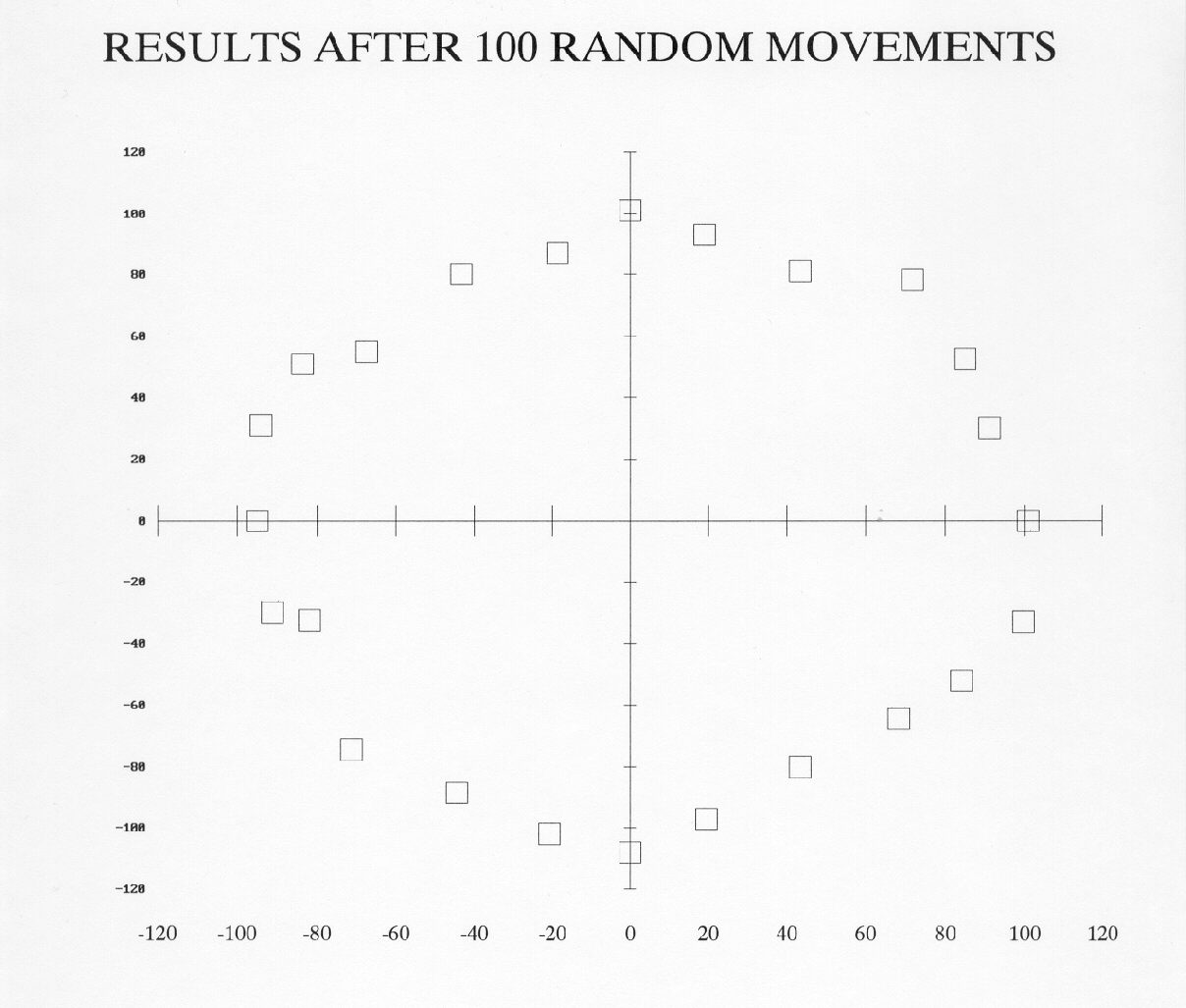 |
In fact, after 500 random moves, we still have a recognizable circle. In this particular case, the circle hasn't even changed shape by fifty percent, in spite of the possibility for it to change by five hundred percent or break down completely. Isn't it remarkable that we can have a complex system in which all the separate entities can move independently and randomly, yet there is a robust persistence of the basic shape! This is a small example of stability in a sea of change.
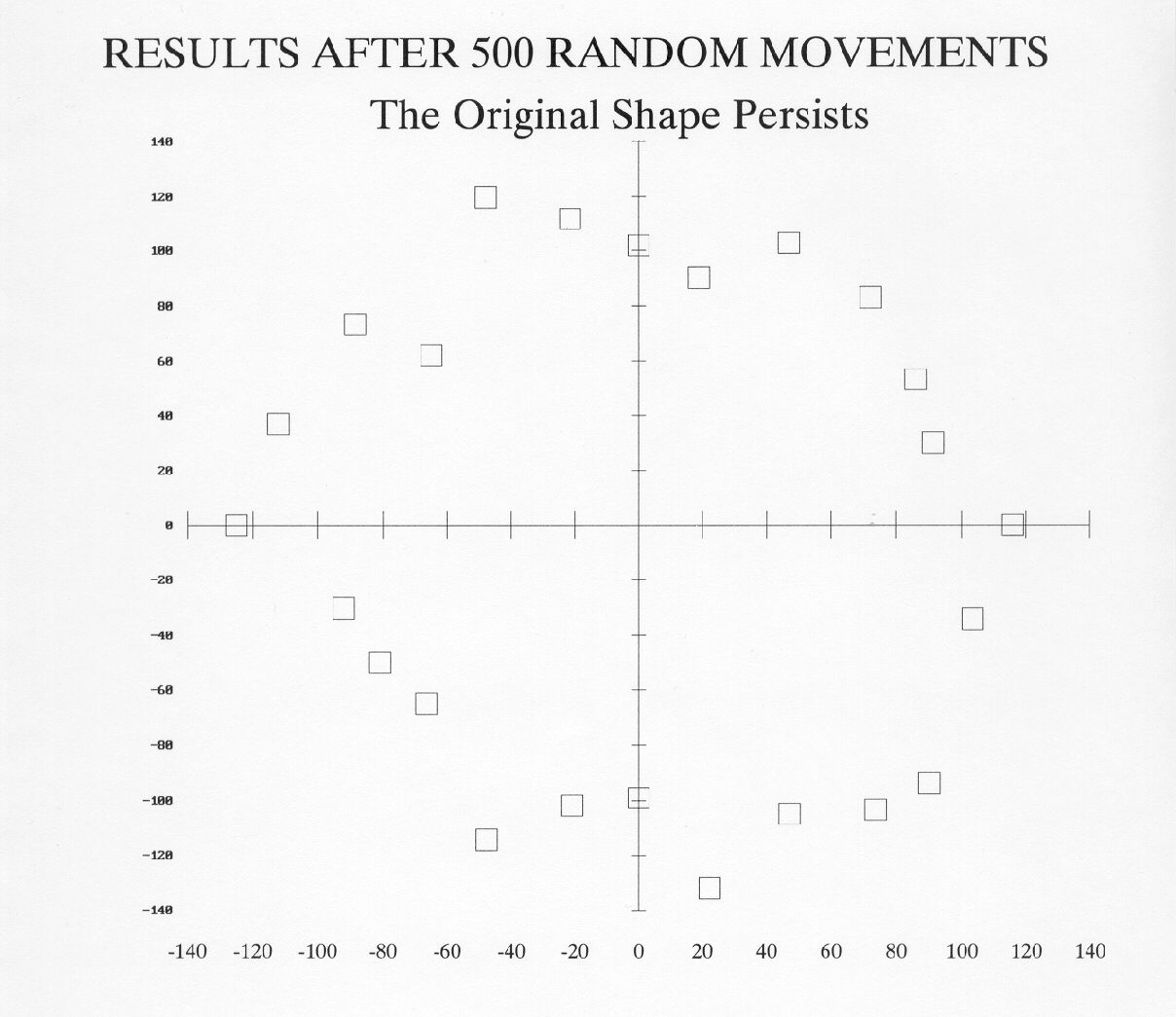 |
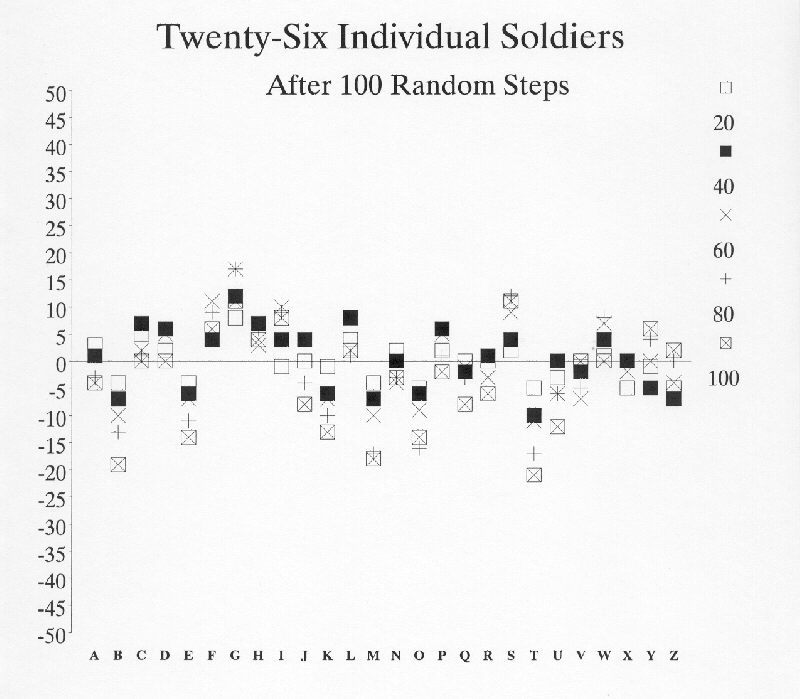
Now let us break the circle and stretch it out into a straight line. We will return to our example of the man in the field, only now let us think in terms of a company of soldiers in a field. Just to pick a number, let us suppose that we have twenty-six soldiers. We will name the soldiers A to Z and graph their ending position after one hundred steps. We can do this time and time again and you will see that much of the time, just like the circle, many of the soldiers are clustered around their starting point at zero.
Although it should be no surprise that occasionally a few of the soldiers wander toward the extremes, even after 500 random steps, most of the soldiers are within 10% of their starting point. In the example below, no soldier has moved more than 60 steps away, out of a possible 500! We begin to understand that a lot of random movement tends to cancel itself out, and not much directional progress is made.
 |
 |
Now let us move from individual random motion to the concept of a system. Almost everything is connected in some way. The universe is made up of multiple systems and subsystems within systems. Connections are what define a system. The connection may be as tenuous as the possibility that a gas molecule could bump into another molecule and be redirected, or it could be a very strong connection based on relational rules.
Let us turn the twenty-six soldiers into a system. Instead of a bunch of individuals acting totally independently, we are going to consider an army with rules, a system of soldiers. We shall devise some very simple relational rules for our army. The basic premise is that we want the army to stay together. The rules are as follows:
- As before, each soldier can only move one step (forward or back), or stay in the same position on each step.
- Before each new step, each soldier must look at his neighbor on his left and his neighbor on his right. No soldier can be more than 2 paces ahead or behind either neighbor. In fact, any soldier that finds himself two paces or more ahead (or behind) any neighbor must move back (or forward) on the next step to compensate.
- If rule 2 does not apply and any soldier is ahead of both neighbors, he can only stay the same or go back on the next step. (Because if he goes forward and the neighbor goes back, rule 2 will be violated.) Likewise, if any soldier is behind both neighbors, he can only stay the same or go forward on the next wing flap.
- If rules 2 and 3 do not apply, then on each step the soldier can do anything he wants (stay in place, go forward, or go back) in accord with rule 1.
Once again we can program the computer to demonstrate how the whole group of soldiers will move. Since every soldier needs to have a neighbor on his left and right, we will assume that the line of soldiers is connected at each end as if arranged in a circle. However, for the ease of display, we will stretch the circle into a straight line on the computer screen. Later on, we can remove this assumption and consider the anomalies that may develop at the boundaries of a system.
We now have an army whose primary objective is to stay together. Within the constraints of that primary objective, the soldiers can still do anything they want. Thus there is no directional motivation for the army (yet). The only mandate is that they work together as a group. If all the soldiers coordinate, the whole army can be one hundred paces forward (or back) at the end of any series of one hundred steps. But if you have ever worked on a committee, you know how hard it is to get cooperation! When you are trying to go forward there is always some yahoo who is going backward. In fact, since our rules say that a soldier can only move more than two steps in any direction if his neighbors move with him, the only way the group can progress is if there is cooperation. As you might guess, it is hard to get cooperation without leadership, or similar motivation among all the individuals.
Let's run the program and graph where the group of soldiers is on the 20th, 40th, 60th, 80th and 100th step. Interestingly, no soldier in the army ever gets more than about 5 paces away from the start point. (Compare with the random movement above.) We can run the series of one hundred steps over and over again, starting from the last ending point; and even after one thousand steps, the group has not been able to progress other than to wander in a very limited range.
 |
Now let's select just one soldier and give him a flag to carry. We will allow the soldier with the flag the opportunity to progress without regard for his neighbors. The motivation of the soldier with the flag is to progress forward toward the enemy. Suddenly we have the classic V formation with the leader (in the middle) pulling the whole group along! Keeping our rules in mind, this result should come as no great surprise. (Since no soldier is allowed to fall more than two meters behind his neighbor, the immediate neighbors to the leader are automatically pulled forward. Then the secondary neighbors are pulled forward, then their neighbors, and their neighbors, etc. throughout the whole company of soldiers.) The real surprise is that we did not change the level of cooperation throughout the army, nor did we assign any new motivation to the individual soldiers. All we did was introduce one leader in order to obtain a very different, organized result.
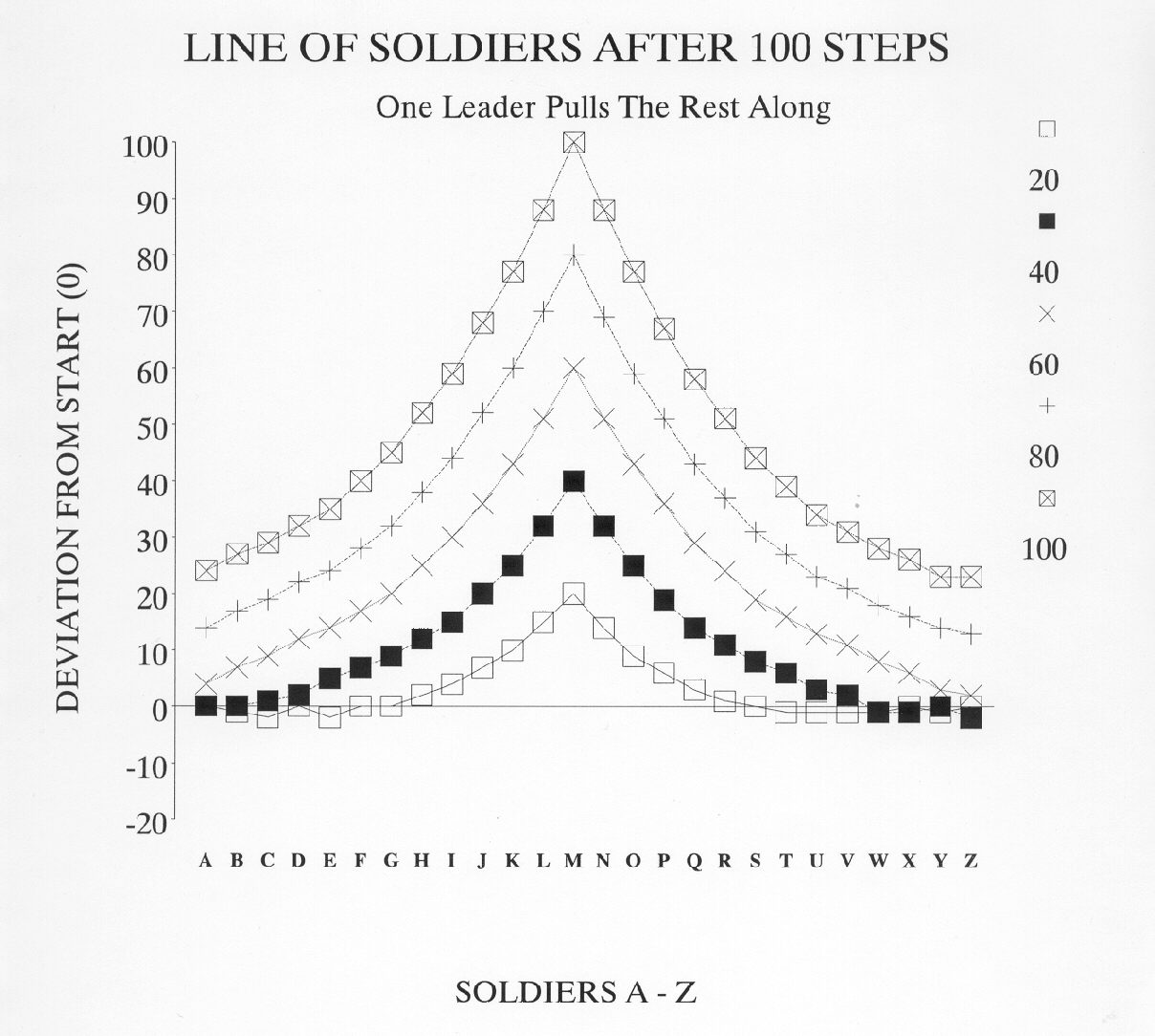 |
Think about the three situations. In case one, we have an unconnected group of soldiers moving randomly and ending up spread over the entire spectrum of possible results. In case two, we connect the soldiers with some very simple rules of interaction that make them behave as a group. We now have a system in which the individuals have some connection, but there is no common purpose and there is no leadership. The result is that most of their individual efforts nullify each other and the army stays concentrated in a fairly small area. In case three, we apply a very limited and concentrated amount of what we call leadership in a social system, or what we might call energy or force in a physical system, and we are able to obtain a very organized result from the whole group. Let me point out, however, that although the introduction of leadership to the army can have a dramatic effect in moving the soldiers forward, an equal, but disturbing effect is seen if we introduce a negative force. Let us suppose one of the soldiers has a physical impediment, or is for some reason recalcitrant (i.e. a coward) and simply moves backward one pace on each step. Under the same rules that connect the individual soldiers into an army, a single 'laggard' soldier can pull the whole army backward as effectively as a single leader can pull the army forward. This result has interesting implications for the social philosopher. At what point does the strength of 'grouping' become a liability?